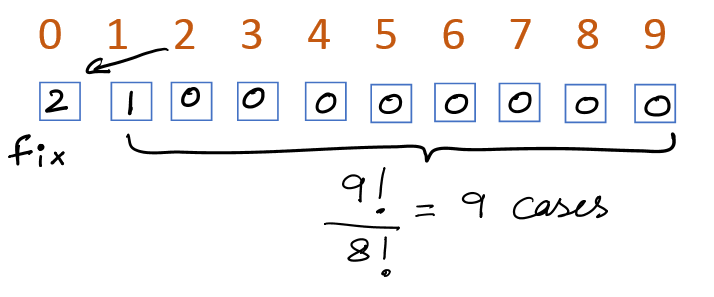Practise Tests
21
Find the total number of ways in which a student can attempt an exam, such that he answers at least two questions out of a total of 150 questions in the exam, given that each question has four multiple answers choices.
Answer : Option D
Explanation:
Video Explanation is given
22
There are N stations on a railroad and every station issues ticket to other station. Some more station are added. Now they have to issue 38 tickets additional or more. What are number of stations before and after adding?
23
If a square is selected at random from 8 x 8 chessboard, what is the probability that the square is of dimension 1 x 1?
Answer : Option C
Explanation:
As we discussed earlier question
The total number of square in a 8 x 8 chessboard is 204.
But in this case we have just counted 1 x 1 squares. What about the 2 x 2 squares, 3 x 3 squares, 4 x 4 squares and so on?
Number of 1 x 1 squares= 8 x 8 = 64
Number of 2 x 2 squares = 7 x 7 = 49
Number of 3 x 3 squares = 6 x 6 = 36
Number of 4 x 4 squares = 5 x 5 = 25
Number of 5 x 5 squares = 4 x 4 = 16
Number of 6 x 6 squares = 3 x 3 = 9
Number of 7 x 7 squares = 2 x 2 = 4
Number of 8 x 8 squares = 1 x 1 = 1
Total number of Squares = 82 + 72 +62 +........... 22 + 12 = 204.
Hence the probability 3 x 3 squares are selected =
24
If the sum of three Natural numbers x, y and z is 10. How many ordered triplets (x, y, z) exist?
Answer : Option C
Explanation:
x + y + z = 10. Now, let us place 10 sticks in a row
| | | | | | | | | |
This question now becomes the equivalent of placing two '+' symbols somewhere between these sticks. For instance
| + | | | + | | | | | |
This would be the equivalent of 1 + 3 + 6. or, x = 1, y = 3, z = 6.
There are 9 gaps between these 10 sticks, out of which one has to select 2 for placing the '+' symbol.
The number of ways of doing this would be 9C2. Bear in mind that this kind of calculation counts ordered triplets. (1, 3, 6) and (6, 3, 1) will both be counted as distinct possibilities. In general, we can also use this formula = sum-1Cn-1= 9C2 = 36.
25
There are 6 tasks and 6 persons. Task 1 cannot be assigned either to person 1 or person 2; task 2 must be assigned to either person 3 or person 4. Every person is to be assigned one task. In how many ways can the assignment can be done?
Answer : Option A
Explanation:
Lets assume that P represents persons and empty boxes represents tasks.
Task 2 can be assigned in 2 ways (either to person 3 or person 4).

Now assume that has occupied his place, then
Task 1 can then be assigned in only 3 ways (persons 4, 5 and 6) as and cannot do the task 1

The remaining 4 tasks can be assigned to the remaining 4 persons in 4! = 24 ways
∴ The assignment can be done in 3 × 2 × 24 = 144 ways
26
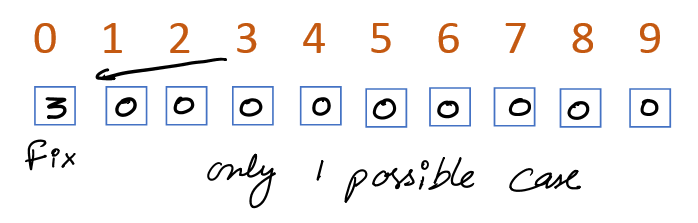
How many 10-digit numbers can be formed such that the sum of the digits of numbers is 3?
Answer : Option B
Explanation:
In this question, given digits are 0 to 9, and the numbers has to be divisible by 3.
If the sum of the digits of a number is divisible by 3 then the number is divisible by 3.
Say: 12549 is divisible by 3, since sum of digits (1 + 2 + 5 + 4 + 9) = 21 / 3
In our question: 10 digits are available, with 10 places.
'0' cannot take the first position, as it is said 10 digit number.
Case 1: Starts with digit 1 and other digits can be ( 2 or 0 ) as sum = 3
Case 2: Starts with digit 2 and other digits can be ( 1 or 0 ) as sum = 3
Case 3: Starts with digit 3 and other digits must be (0) as sum = 3
Hence the total numbers formed are 9 + 36 + 9 + 1 = 55
27
How many five digit numbers can be formed by using the digits 0, 1, 2, 3, 4, 5 such that the number is divisible by 4?
28
Two identical cubes if one of them is painted green on its 4 sides and yellow on the remaining two side then how many faces painted green to other cube so that probability of getting the same color is 1/3 when we roll both the cubes?
Answer : Option C
Explanation:
First cube is painted with 4 green sides and 2 yellow sides.
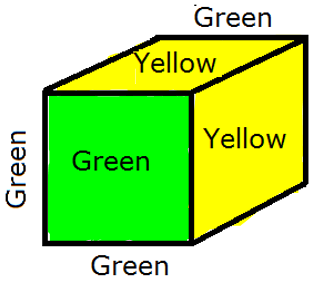
Let the other cube have x sides with green and (6 - x) sides painted with yellow sides.
As per condition in the given question, when we roll both the dice, we can should have either green on both cubes or yellow on both cubes.
4 green 2 yellow
X green (6 – X) yellow
Both green or both yellow
( which is already given in the question)
x = 0
So second cube should not have any green faces.
29
How many three digit numbers can be formed using the digits 0, 1, 2, 3, 4, 5 (repetition is not allowed) such that the number is divisible by 15?
Answer : Option C
Explanation:
For divisible by 15, the number can be divided by 3 and 5.
Divisible by 5, it should end with 0 or 5
Divisible by 3, (Sum of the digits) / 3
Case 1: The number is ending with 5 and the remaining places 0 cannot occupy
, 1, 2, 3, 4, 5
_1_ _0_ _5_
_1_ _3_ _5_
_3_ _1_ _5_
_3_ _4_ _5_
_4_ _0_ _5_
_4_ _3_ _5_
Here the total 6 numbers can be formed.
Case 2: The number is ending with 0
0, 1, 2, 3, 4, 5
_1_ _2_ _0_
_1_ _5_ _0_
_2_ _1_ _0_
_2_ _4_ _0_
_4_ _2_ _0_
_4_ _5_ _0_
_5_ _1_ _0_
_5_ _4_ _0_
Here, 8 numbers can be formed.
Total = 6 + 8 = 14 numbers
30
There are 11 alphabets A, H, I, M, O, T, U, V, W, X, Y. They are called symmetrical alphabets. The remaining alphabets are known as asymmetrical alphabets. How many four-lettered passwords can be formed by using symmetrical letters only? (repetitions not allowed)
Answer : Option C
Explanation:
Given 11 alphabets A, H, I, M, O, T, U, V, W, X, Y.
4 out of the 11 symmetrical alphabets need to be selected,
Also the order of alphabets needs to be taken into account (as it is a password)
∴ 11P4 = 7920.
Hence, option 3.