Practise Tests
11
How many 3 digit numbers can be formed with 2 exactly consecutive same numbers?
Answer : Option D
Explanation:
Here in the 3-digit number, in which two consecutive digits are same like 223, 551, 500 and so on ..... but not 111, 222 ... as it is mentioned exactly 2 digits same not 3 digits.
Case I:
Let us assume that the and positions are same, then it can be done in 10 ways like given below:

position can take values from 1 to 9 only ( zero cannot be occupy).Therefore total ways comes out to b 9 x 10 = 90 ways.
Case I:
Let us assume that the and positions are same as '0' cannot be occupied, then it can be done in 9 ways like given below:

position can take values from 1 to 10 (zero can occupy).Therefore total ways comes out to b 9 x 10 = 90 ways.
Total = 90 + 90 = 180 numbers.
Now remove these 9 common numbers like 111, 222, 333 ...... 999) from both cases.
Therefore finally 180 - 18 = 162
12
A bag contains 8 coins of denominations 5 rupee, 1 rupee, 50 paise, 25 paise, 10 paise, 3 paise, 2 paise and 1 paise respectively. How many different sums of money can formed?
Answer : Option C
Explanation:
Here 8 coins are given:
5 rupee, 1 rupee, 50 paise, 25 paise, 10 paise, 3 paise, 2 paise and 1 paise.

Pick 1 coin from the above 8 coins, then we get 8 different values 5 rupee or 1 rupee or 50 paise or 25 paise or 10 paise or 3 paise or 2 paise or 1 paise = 8C1= 8 ways
Pick 2 coins from the above 8 coins = 8C2= 28 ways
We can get
Rs.5 + Rs.1 = Rs.6
Rs.5 + 50 paise = Rs.5.50
Rs.5 + 25 paise = Rs.5.25
.
Rs.1 + 10 paise = Rs.1.10 and so on.
Pick 3 coins from the above 8 coins = 8C3 = 56 ways
We can get
Rs.5 + Rs.1 + 50 paise = Rs.6.50
Rs.5 + Rs.1 + 25 paise = Rs.6.25
Rs.1 + 50 paise + 10 paise = Rs.1.60...so on.
...
Pick 4 coins
....
Pick 5 coins ...... Pick all 8 coins = 8C8 = 1 way
Hence the answer is
= 8C1 + 8C2 + 8C3 + 8C4 + 8C5 + 8C6 + 8C7 + 8C8
= 255 ways
13
How many three digit number formed by using 2, 3, 4, 5, 6, 7 such that number is divisible by 15 ( repetition of digits is not allowed)
Answer : Option D
Explanation:
For divisible by 15, the number can be divided by 3 and 5.
Divisible by 5, it should end with 0 or 5
Divisible by 3, (Sum of the digits) / 3
Now 0 is not available, so 5 can occupy the last place.
2, 3, 4, 5, 6, 7
_3_ _4_ _5_
_3_ _7_ _5_
_4_ _3_ _5_
_4_ _6_ _5_
_6_ _4_ _5_
_6_ _7_ _5_
_7_ _3_ _5_
_7_ _6_ _5_
Hence the total 8 numbers can be formed.
14
How many numbers can be formed using the digits (1, 2, 3, 4, 5, 6, 7, 8, 9) such that the numbers are in increasing order. ( repetition of digits is not allowed)?
Answer : Option A
Explanation:
There are different cases involved in these
9 digit numbers
Do not remove any digit, it will be increasing order
(123456789)
8 digit numbers
Remove any 1 digit from the given 9 digit

Here we can remove any 1 digit from these 9 digits = 9C1= 9 ways
7 digit numbers
Remove any 2 digit from the given 9 digit

Here we can remove any 2 digit from these 9 digits = 9C2= 36 ways
In the same manner, we can remove any 3 digits, 4 digits, 5 digits and so on ...... we can remove till 7 digits.
= 9C0+9C1+9C2+9C3+9C4+9C5+9C6+9C7
= 1 + 9 + 36 + 84 + 126 + 126 + 84 + 36
= 502 Numbers
15
A lady gives a dinner party to her six guests. The number of ways in which they may be selected from among ten friends, if two particular friends will not attend the party together is ?
Answer : Option B
Explanation:
Suppose lady has A, B, C, D, E, F, G, H, I, J are 10 friends.
Let us say A and B are enemies and not willing to come together.
Case I: If A is interested then B is not interested, then
choosing 6 guests form 9 person can be done
A, C, D, E, F, G, H, I, J = = 84 ways
Case II: If B is interested then A is not interested, then
choosing 6 guests form 9 person can be done
A, C, D, E, F, G, H, I, J = = 84 ways.
But remember, there are 8 people like C, D, E, F, G, H, I, J ( who are repeated in both cases, So remove them) = = 28 ways.
So the final combination is = 140 ways
16
In a chess competition involving some boys and girls of a school, every student had to play exactly one game with every other student. It was found that in 45 games both the players were girls, and in 190 games both were boys. The number of games in which one player was a boy and the other was a girl is?
Answer : Option A
Explanation:
Video Explanation is given
Answer : Option 1
Explanation:
17
How many 6 digit numbers can be formed using the digits 0 to 5 (without repetition) such that the number is divisible by the digit at its units place?
Answer : Option D
Explanation:
For the six digit numbers using 0, 1, 2, 3, 4 and 5
0 cannot occupy the first and last position as the 6-digit number cannot be formed.
18
A box contains 3 red and 2 white balls and the balls are taken at random one by one without replacement. What is the probability that the ball drawn at the last is a white ball?
Answer : Option D
Explanation:
From 3 red balls and 2 white balls.
Keep 1 white ball fix in the end.
then, there are four balls left (i.e) 3 red and 1 white balls left
resulting 4 combinations
W R R R
R W R R
R R W R
R R R W
4 cases x =
19
How many 4 digit numbers can be formed using the digits 0 to 9 such that atleast two digits are same?
Answer : Option C
Explanation:
In this question, he asked about atleast 2 digits same (i.e) we can have more than 2 digits also.
For any number formed, we have possibilities:
No digit same + 2 digits same + 3 digits same + 4 digits same = Total numbers formed.

For example:
1234 , 1123, 1113, 1111
we don't need 1234 kind of numbers, and the rest of all type of numbers are accepted.
Therefore, it is possible, if we subtract
Total possible numbers with repetition - Without repetition
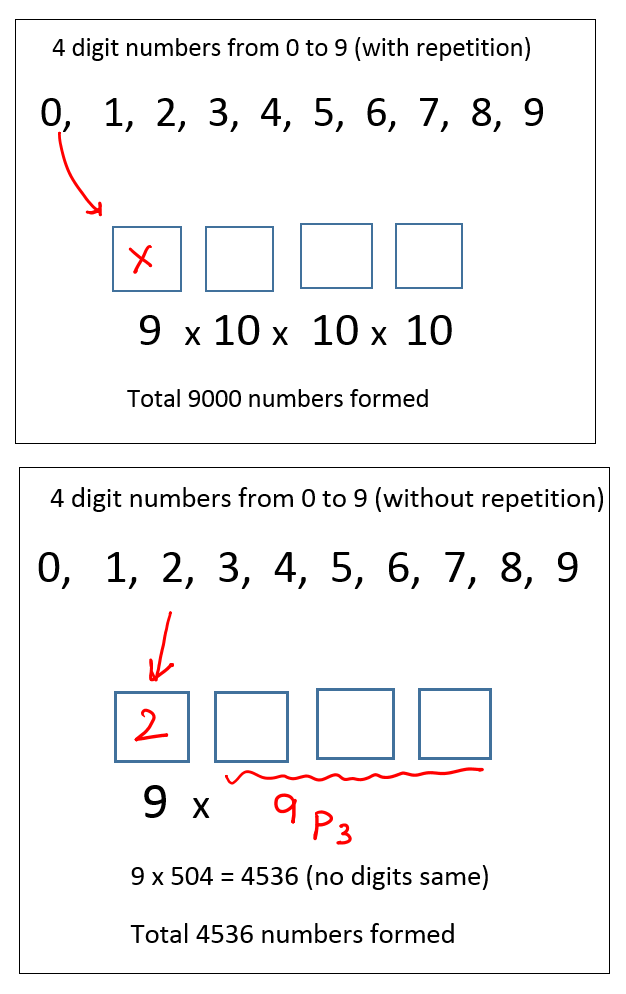
So atleast 2 digits same = With repetition - Without repetition
= 9000 - 4536
= 4464
20
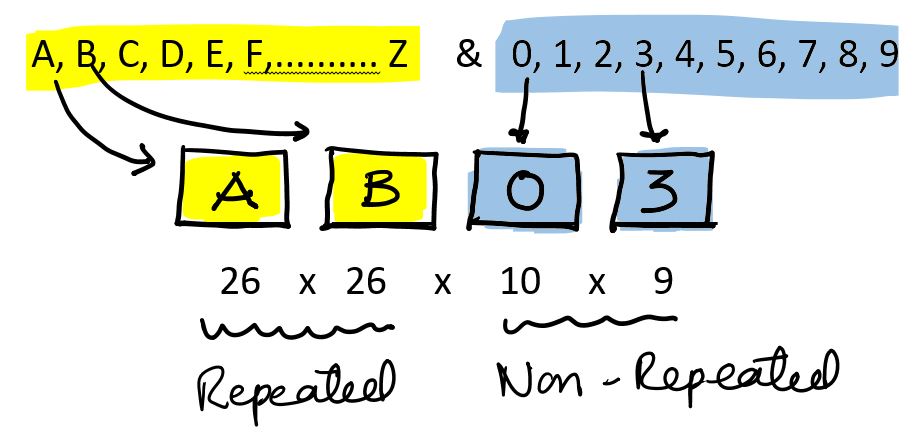
How many number plates can be formed, if the number plates have two letters of english alphabet and followed by a two digit number, if repetition of digits is not allowed.
Answer : Option D
Explanation:
In this question, it is asked about four digit number plate, in which first two digits are alphabets ( letters ) and the next two are digits.
Remember : It is also said that repetition of digits is not allowed ( means only digits not alphabets
Available items are
Therefore the total number of number plates formed is 60840