Practise Tests
1
How many squares can be chosen from an 8 x 8 chessboard?
Answer : Option D
Explanation:
In a 8 x 8 chessboard ( grid ) given below

We have 1 x 1 squares, 2 x 2 squares,3 x 3 squares,4 x 4 squares ......................... 8 x 8 squares.
So, the number of total square in a N x N grid is
.
Hence for the 8 x 8 chessboard, total type of squares
.
1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 = 204
2
How many rectangles can be formed in a grid of 5 x 6 ?
Answer : Option C
Explanation:
This can be done by using a formula:
The number of rectangles formed in a m x n grid is given by
( 1 + 2 + 3 + 4 ...... m ) x ( 1 + 2 + 3 + 4 ...... n ), where m & n are the size of the grid.
In our question, it is given the 5 x 6 grid means
m = 5 and n = 6
So, the number of rectangles
( 1 + 2 + 3 + 4 + 5 ) x ( 1 + 2 + 3 + 4 + 5 + 6 )
( 15 ) x ( 21 )
315 rectangles are formed
3
The probability that a square selected at random from a 8 x 8 chessboard is of size 3 x 3 is
Answer : Option C
Explanation:
As we discussed earlier question[1]
The total number of square in a 8 x 8 chessboard is 204.
But in this case we have just counted 1 x 1 squares. What about the 2 x 2 squares, 3 x 3 squares, 4 x 4 squares and so on?
Number of 1 x 1 squares= 8 x 8 = 64
Number of 2 x 2 squares = 7 x 7 = 49
Number of 3 x 3 squares = 6 x 6 = 36
Number of 4 x 4 squares = 5 x 5 = 25
Number of 5 x 5 squares = 4 x 4 = 16
Number of 6 x 6 squares = 3 x 3 = 9
Number of 7 x 7 squares = 2 x 2 = 4
Number of 8 x 8 squares = 1 x 1 = 1
Total number of Squares = = 204.
Hence the probability 3 x 3 squares are selected = =
4
In how many ways is it possible to choose a white square and a black square on a chess board so that the squares must not lie in the same row or column?
Answer : Option D
Explanation:
The white square can be chosen in 32 ways.
If we remove the row and the column which contains the chosen white square, we will be left with 7 Rows & 7 Columns containings a total of 49 squares (24 black, 25 whites)
Say, initially we choose White square (W1), then from the 7 x 7 remaining square, we have to select any black square ( 24 possibilities)
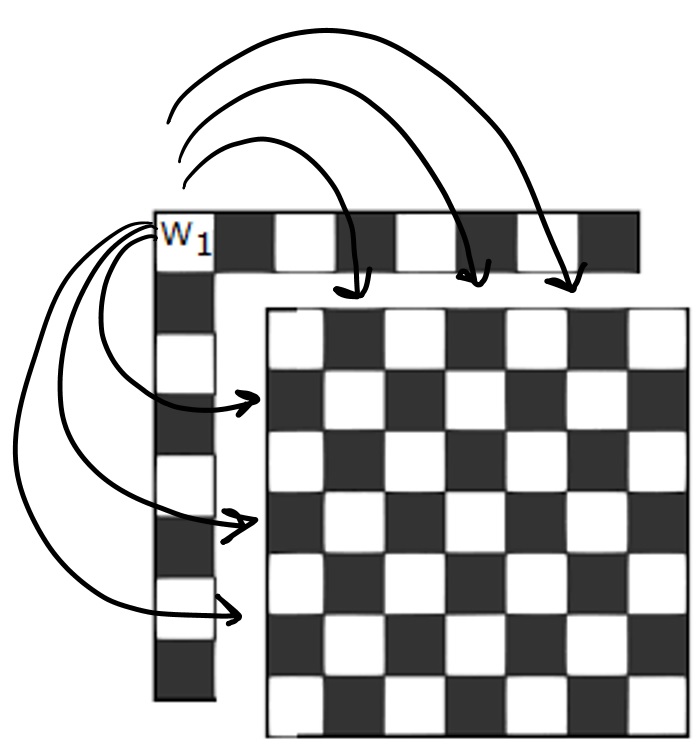
So each W1 x 24 black squares,
therefore, each white square x 24 possibilities
Required ways = 32 x 24 = 768
5
The figure below show the plan of a town. The streets are right angles to each other. A rectangular park (P) is situated inside a town with a diagonal road running through it. There is also prohibited region (D) in the town?
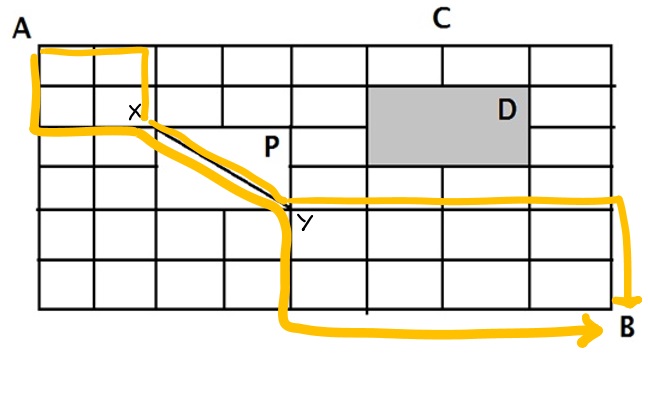
If Neelam rides her bicycle from her house at A to her office at B, taking the shortest path. Then the number of shortest paths that she can choose is
Answer : Option A
Explanation:
If Neelam wants to reach B in the shortest possible path, then she has to travel in the diagonal path say ( X Y)
(i.e) ( A X) ( X Y) and finally ( Y B)
Below diagram shows the partially routes
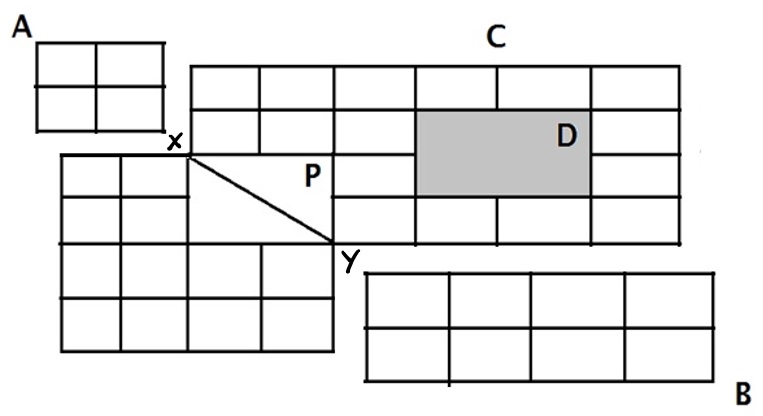
Let us take ( AX), here we can see the grid is ( 2 x 2 )
Number of ways = = = 6 ways
Let us take ( XY), here we have one straight diagonal path
Number of ways = 1 way.
Let us take ( BY), here we can see the grid is ( 2 x 4 )
Number of ways = = = 15 ways
Therefore, the total number of paths possible = 6 x 1 x 15 = 90 ways.
6
How many 5-digit numbers can be formed using the digits 0, 2, 4, 6 and 8 such that the numbers are divisible by 8, ( repetition of digits is not allowed)
Answer : Option B
Explanation:
For any given number to be divisible by 8, its last three digits must divisible by 8.
So, last three digits can be from the following condition:
(024), (048), (064), (208), (240), (248), (264), (280), (408), (480), (608), (624), (640), (648), (680), (824), (840), (864),
There are total 18 such cases.
Now, Consider these 12 cases in which zero is there
(024), (048), (064), (208), (240), (280), (408), (480), (608), (640), (680), (840)
Lets the number ends with 0 2 4

With each of these 12 cases, first digit can be any of the remaining 2 digits and second digit can be the remaining one digit
Therefore, 12 × 2! = 24 such numbers
Consider the 6 cases in which zero does not come.
(248), (264), (624), (648), (824), (864)
Lets the number ends with 2 4 8
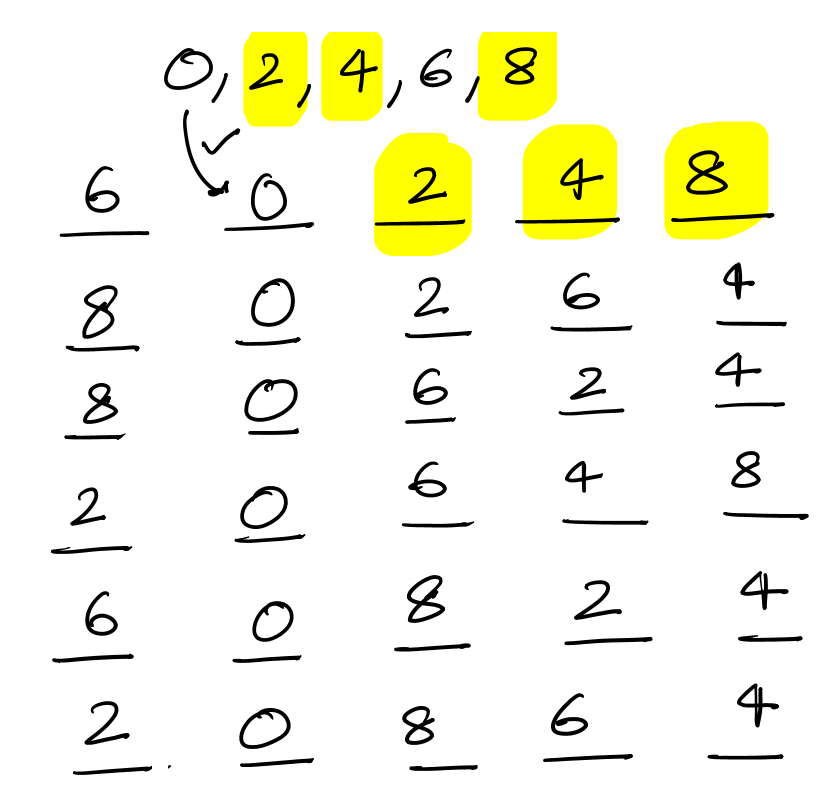
With each of these 6 groups, first digit can be the one remaining digit(because zero cannot be the first digit)
Second digit can be zero
Therefore, 6 × 1 = 6 such numbers
Hence total numbers formed 24 + 6 = 30
7
How many 6-digit numbers can be formed using the digits 1 to 6, without repetition such that the number is divisible by the digit in its units place?
Answer : Option C
Explanation:
The explanation is given in the Video
Answer : Option 3
Explanation:
8
What is the sum of all five digit numbers that can be formed using the digits 1, 2, 3, 4 and 5 without repetition?
Answer : Option A
Explanation:
In general, the sum of the digits is given by
(n - 1)! x (111...1 n times) x (sum of digits), where n is number of digits
So the given digits are 1, 2, 3, 4 and 5
(5 - 1)! x (11111) x (1+2+3+4+5)
(4)! x (11111) x (15)
(24) x (11111) x (15)
3999960
9
Sherlock Homes and Dr. Watson have to travel from Rajiv Gandhi Chowk to Indira Gandhi International Airport via the Metro. They have enough coins of 1, 5, 10 and 25 paise coins. Sherlock Homes agrees to pay for Dr. Watson, only if tells all the possible combination of coins that can be used to pay for the ticket.
How many combinations are possible, if the fare is 50 paise?
Answer : Option B
Explanation:
The total 50 paise can be paid using these coins:
With any one type coins
50(1 paise)
10(5 paise)
5(10 paise)
2(25 paise)
total 4 ways -----(1)
With any two type coins
5(1 paise), 9(5 paise)
10(1 paise), 8(5 paise)
15(1 paise), 7(5 paise)
...
45(1 paise), 1(5 paise) (9 ways)
10(1 paise), 4(10 paise)
20(1 paise), 3(10 paise)
30(1 paise), 2(10 paise)
40(1 paise), 1(10 paise) (4 ways)
25(1 paise), 1(25 paise) (1 ways)
2(5 paise), 4(10 paise)
4(5 paise), 3(10 paise)
6(5 paise), 2(10 paise)
8(5 paise), 1(10 paise) (4 ways)
5(5 paise), 1(25paise) (1 way)
10 and 25 can not be used alone
Total number of options = 9+4+1+4+1 = 19 ways
With any three type coins
5(1 paise), 1(5 paise), 4(10 paise)
5(1 paise), 3(5 paise), 3(10 paise)
5(1 paise), 5(5 paise), 2(10 paise)
5(1 paise), 6(5 paise), 1(10 paise)
10(1 paise), 2(5 paise), 3(10 paise)
10(1 paise), 4(5 paise), 2(10 paise)
10(1 paise), 6(5 paise), 1(10 paise)
15(1 paise), 1(5 paise), 3(10 paise)
15(1 paise), 3(5 paise), 2(10 paise)
15(1 paise), 5(5 paise), 1(10 paise)
20(1 paise), 2(5 paise), 2(10 paise)
20(1 paise), 4(5 paise), 1(10 paise)
25(1 paise), 1(5 paise), 2(10 paise)
25(1 paise), 3(5 paise), 1(10 paise)
30(1 paise), 2(5 paise), 1(10 paise)
35(1 paise), 1(5 paise), 1(10 paise) (total 16 ways)
5(1 paise), 4(5 paise), 1(25 paise)
10(1 paise), 3(5 paise), 1(25 paise)
15(1 paise), 2(5 paise), 1(25 paise)
20(1 paise), 1(5 paise), 1(25 paise) (4 ways)
5(1 paise) 2(10 paise) 1(25 paise)
15(1 paise) 1(10 paise) 1(25 paise) (2 ways)
1(5 paise), 2(10 paise), 1(25 paise)
3(5 paise), 1(10 paise), 1(25 paise) (2 ways)
Total number of options = 16+4+2+2 = 24 ways
With all type coins
5(1 paise), 2(5 paise), 1(10 paise), 1(25 paise)
10(1 paise), 1(5 paise), 1(10 paise), 1(25 paise)
Total = 2 ways
Required number of combinations = 4+19+24+2 = 49
10
In how many ways can 10 chocolates can be distributed among 6 children so that each gets at least one present.
Answer : Option A
Explanation:
No of ways of dividing n identical things among r different group
(for non empty set i.e, each one get at least one) is given by (n-1) C (r-1)
so on applying this to given situation we get 9C5
